퀵 정렬
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
퀵 정렬은 1959년 토니 호어에 의해 개발된 효율적인 정렬 알고리즘으로, 분할 정복 방식을 사용한다. 리스트를 피벗을 기준으로 분할하고 재귀적으로 정렬하는 방식으로, 평균 시간 복잡도는 O(n log n)이지만 최악의 경우 O(n^2)가 될 수 있다. 퀵 정렬은 유닉스 시스템의 기본 정렬 함수로 채택되었으며, C 표준 라이브러리의 qsort 함수와 자바의 참조 구현에도 영향을 미쳤다. 퀵 정렬의 성능은 피벗 선택 방식에 따라 달라지며, 다양한 최적화 기법과 변형이 존재한다. 퀵 정렬은 다른 정렬 알고리즘과의 관계 속에서 힙 정렬, 병합 정렬 등과 비교되며, C 언어 등 다양한 프로그래밍 언어로 구현될 수 있다.
토니 호어가 1959년 모스크바 대학교에서 방문 연구원으로 있을 때 퀵 정렬 알고리즘을 개발했다. 당시 호어는 영국 국립 물리 연구소를 위해 기계 번역 프로젝트를 진행하고 있었다. 번역 과정의 일부로, 러시아어 문장의 단어를 러시아-영어 사전에서 찾아보기 전에 정렬해야 했는데, 이 사전은 자기 테이프 데이터 저장에 알파벳 순서로 저장되어 있었다.[5] 호어는 첫 아이디어인 삽입 정렬이 느리다는 것을 깨달은 후, 새로운 아이디어를 떠올렸다.
퀵 정렬은 분할 정복(divide and conquer) 방법을 통해 리스트를 정렬한다.[11]
개의 리스트를 정렬하는데 걸리는 시간을 , 를 임의의 상수라 하고, 리스트가 두 개의 거의 같은 부분집합으로 나뉜다고 가정하면 평균 시간 복잡도는 다음과 같다.
2. 역사
호어는 Mercury 오토코드로 분할 부분을 작성했지만, 정렬되지 않은 세그먼트의 목록을 처리하는 데 어려움을 겪었다. 영국으로 돌아온 후 셸 정렬에 대한 코드를 작성해 달라는 요청을 받았다. 호어는 상사에게 더 빠른 알고리즘을 알고 있다고 말했고, 상사는 그가 모른다는 데 6펜스를 걸었다. 결국 상사는 그가 내기를 졌다는 것을 인정했다.
호어는 컴퓨터 저널 [https://academic.oup.com/comjnl/article/5/1/10/395338?login=false 1962년 5권 1호, 10-16페이지]에 자신의 알고리즘에 대한 논문을 발표했다. 이후 ALGOL과 재귀 기능을 알게 되었고, 이를 통해 개선된 알고리즘 버전을 당시 최고의 컴퓨터 과학 저널인 ''Communications of the Association for Computing Machinery''에 ALGOL로 발표했다.[2][6] ALGOL 코드는 [https://dl.acm.org/doi/pdf/10.1145/366622.366642 ACM 통신 (CACM), 1961년 7월 4권 7호, 321페이지 알고리즘 63: 분할 및 알고리즘 64: 퀵 정렬]에 게재되었다.
퀵 정렬은 널리 채택되어, 유닉스에서 기본 라이브러리 정렬 서브루틴으로 나타났다. 따라서, C 표준 라이브러리와 자바의 참조 구현에 이름을 빌려주었다.[15]
로버트 세지윅의 1975년 박사 학위 논문은 퀵 정렬 연구의 이정표로 여겨진다. 그는 샘플 정렬, 반 에민의 적응적 분할[7]을 포함한 다양한 피벗 선택 방식의 분석과 예상 비교 및 교환 횟수의 도출과 관련된 많은 미해결 문제를 해결했다.[15] 존 벤틀리와 더글러스 맥길로이는 1993년에 동일한 요소를 처리하는 기술과 ''아홉 개의 유사 중앙값''으로 알려진 피벗 방식을 포함하여 프로그래밍 라이브러리에서 사용할 수 있도록 다양한 개선 사항을 통합했다.[15]
3. 알고리즘
1. 리스트 가운데서 하나의 원소('''피벗''')를 고른다.
2. 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다. ('''분할''') 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.
3. 분할된 두 개의 작은 리스트에 대해 재귀(Recursion)적으로 이 과정을 반복한다. 재귀는 리스트의 크기가 0이나 1이 될 때까지 반복된다.
재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.
퀵 정렬은 피벗 값을 기준으로 좌우로 나누어 정렬하는 방식이다. 피벗보다 큰 값은 피벗의 왼쪽에, 작은 값은 오른쪽에 위치시킨다. 이 과정을 재귀적으로 반복하면 정렬이 완료된다.
좀 더 구체적으로 설명하면 다음과 같다.
1. 피벗보다 큰 값을 피벗 위치보다 왼쪽에서 찾는다. (i 인덱스 증가)
2. 피벗보다 작은 값을 피벗 위치보다 오른쪽에서 찾는다. (j 인덱스 감소)
3. i 값이 j 값보다 작거나 같으면, 피벗을 기준으로 교환해야 할 값이 있다는 의미이므로 교환 후 i, j 인덱스를 각각 증가, 감소시킨다.
4. i 인덱스가 j 인덱스보다 작거나 같을 때까지 반복한다.
이 과정은 피벗을 기준으로 왼쪽으로 정렬된 리스트에서는 왼쪽 값이 감소된 j보다 작을 때까지, 오른쪽으로 정렬된 리스트에서는 오른쪽 값이 증가된 i 값보다 클 때까지 재귀적으로 반복된다.
퀵 정렬 알고리즘은 분할과 정복 단계를 거치므로 정확성도 그 두 단계를 각각 증명한다. 분할이 정확하다는 것은 임의의 수 x와 배열 형태의 n개의 자료가 주어졌을 때, x 이상의 값을 가지는 것들 중 최솟값 이후로 오직 x 이상의 값을 가지는 자료들만을 몰아서 놓을 수 있다는 것을 의미한다.
증명 방법은 수학적 강귀납법이다.
1. 임의의 수 x와 1개의 자료가 주어지면, 그 유일한 자료의 값이 x 미만이거나 이상이다. 미만이면 x 이상의 값을 가지는 것들이 없으므로 명제는 참이다. 이상이면 x 이상의 값을 가지는 것들이 x뿐이므로 x 이후에 그런 자료들이 놓여 있다.
2. k개 이하의 자료가 주어져도 명제가 성립한다고 가정한다.
3. k+1개의 자료가 주어지면, 가장 처음 자료의 값이 x 미만이거나 이상이다.
자료 배열의 원소 수가 유한하므로, x가 자료 중 하나의 값일 경우 x 이상의 값을 가지는 것들 중 최솟값은 항상 찾을 수 있다. 퀵 정렬 알고리즘은 분할 결과로 x 이상의 값을 가지는 것들 중 최솟값의 배열 상 위치를 함께 표시하여 정렬 대상에서 제외한다. 그러므로 알고리즘이 무한히 반복되지 않음을 보장한다.
퀵 정렬은 다음과 같은 순서로 진행된다.
1. 피벗 선택: 적당한 값(피벗)을 경계값으로 선택한다.
2. 배열 분할: 피벗 미만의 요소를 배열의 앞쪽에 모으고, 피벗 미만의 요소만 포함하는 구간과 그 외로 분할한다.
3. 재귀: 분할된 구간에 대해 다시 피벗 선택과 분할을 수행한다.
4. 정렬 종료: 분할 구간이 정렬되어 있으면 재귀를 중단한다.
3. 1. 분할 방식
퀵 정렬의 핵심은 피벗을 기준으로 리스트를 효율적으로 분할하는 것이다. 퀵 정렬에서는 리스트 가운데서 하나의 원소(피벗)를 고른다. 피벗 앞에는 피벗보다 값이 작은 모든 원소들이 오고, 피벗 뒤에는 피벗보다 값이 큰 모든 원소들이 오도록 피벗을 기준으로 리스트를 둘로 나눈다. 이렇게 리스트를 둘로 나누는 것을 '''분할'''이라고 하며, 분할을 마친 뒤에 피벗은 더 이상 움직이지 않는다.[11]
분할은 다음과 같은 방식으로 이루어진다.
1. 피벗(p)을 선택하고, 리스트 왼쪽 끝과 오른쪽 끝에서 시작한 인덱스들을 i, j라고 한다.
2. 리스트 왼쪽에 있는 i 위치의 값이 피벗 값보다 크고, 오른쪽에 있는 j 위치의 값은 피벗 값보다 작으면 둘을 교환한다.
3. j 위치의 값이 피벗 값보다 작지만, i 위치의 값도 피벗값보다 작으면 교환하지 않는다.
4. i위치를 피벗 값보다 큰 값이 나올 때까지 진행해 j 위치의 값과 교환한다.
5. i위치가 j 위치보다 커지면, i 위치의 값과 피벗 값을 교환한다.
이 과정을 통해 피벗 값 좌우의 리스트는 각각 퀵 정렬을 재귀적으로 수행하여 정렬된다.
두꺼운 선으로 둘러싸인 원소는 피벗 원소로서, 분할의 마지막 원소로 한 경우이다.
다양한 분할 방식이 존재하며, 다른 예시로는 다음과 같은 방법들이 있다.
분할 후 요소 수가 일정 임계값을 밑돌면 삽입 정렬과 같이 "소수의 요소에 대해 더 효율적인 정렬"로 전환하는 기법이 있다. 또한, 배열의 분할 방법 자체에도 다양한 변형이 있다.
3. 1. 1. 로무토 분할 방식 (Lomuto partition scheme)
니코 로무토(Nico Lomuto)가 개발한 분할 방식으로, 구현이 간단하여 퀵 정렬을 설명하는 입문 자료에 자주 사용된다. 이 방식은 배열의 마지막 요소를 피벗으로 선택한다.[11]
```
'''algorithm''' quicksort(A, lo, hi) '''is'''
''// 인덱스가 올바른 순서인지 확인''
'''if''' lo >= hi || lo < 0 '''then'''
return
''// 배열을 분할하고 피벗 인덱스를 가져온다''
p := partition(A, lo, hi)
''// 두 파티션을 정렬한다''
quicksort(A, lo, p - 1) ''// 피벗의 왼쪽''
quicksort(A, p + 1, hi) ''// 피벗의 오른쪽''
''// 배열을 두 파티션으로 나눈다''
'''algorithm''' partition(A, lo, hi) '''is'''
pivot := A[hi] ''// 마지막 요소를 피벗으로 선택''
''// 임시 피벗 인덱스''
i := lo
'''for''' j := lo '''to''' hi - 1 '''do'''
''// 현재 요소가 피벗보다 작거나 같으면''
'''if''' A[j] <= pivot '''then'''
''// 현재 요소와 임시 피벗 인덱스의 요소를 교환한다''
swap A[i] '''with''' A[j]
''// 임시 피벗 인덱스를 앞으로 이동시킨다''
i := i + 1
''// 피벗을 마지막 요소와 교환한다''
swap A[i] '''with''' A[hi]
'''return''' i ''// 피벗 인덱스''
```
이 방식은 를 인덱스로 유지하며, 다른 인덱스 를 사용하여 배열을 스캔한다. 부터 까지 (포함) 요소는 피벗보다 작고, 부터 까지 (포함) 요소는 피벗과 같거나 크다. 이 방식을 사용하면 배열이 이미 정렬된 경우 최악의 분할로 인해 퀵 정렬의 복잡성이 로 저하된다.[9]
전체 배열을 정렬하려면 을 실행한다.
3. 1. 2. 호어 분할 방식 (Hoare partition scheme)
토니 호어 경이 제안한 분할 방식은 배열의 양쪽 끝에서 시작하여 서로를 향해 이동하는 두 개의 포인터(인덱스)를 사용한다. 피벗보다 큰 값을 첫 번째 포인터에서, 피벗보다 작은 값을 두 번째 포인터에서 찾을 때까지 이동한다. 만약 첫 번째 포인터가 두 번째 포인터보다 앞에 있다면, 이 요소들은 서로 잘못된 순서에 있으므로 교환된다.[13] 이후 포인터는 안쪽으로 이동하며 역전 검색이 반복된다. 포인터가 교차하면(첫 번째 포인터가 두 번째 포인터 뒤에 위치) 교환은 중단되고, 유효한 분할이 이루어진다. 분할 지점은 교차된 포인터 사이가 된다.
의사 코드는 다음과 같다.[12]
```
''// 배열의 일부를 정렬하고, 분할 후 다시 정렬''
'''알고리즘''' 퀵 정렬(A, lo, hi) '''는'''
'''if''' lo >= 0 && hi >= 0 && lo < hi '''then'''
p := partition(A, lo, hi)
quicksort(A, lo, p) ''// 피벗 포함''
quicksort(A, p + 1, hi)
''// 배열을 두 부분으로 분할''
'''알고리즘''' partition(A, lo, hi) '''is'''
''// 피벗 값''
pivot := A[lo] ''// 첫 요소를 피벗으로 선택''
''// 왼쪽 인덱스''
i := lo - 1
''// 오른쪽 인덱스''
j := hi + 1
'''loop forever'''
''// 왼쪽 인덱스를 최소 한 번 오른쪽으로 이동, 피벗보다 작은 동안 반복''
'''do''' i := i + 1 '''while''' A[i] < pivot
''// 오른쪽 인덱스를 최소 한 번 왼쪽으로 이동, 피벗보다 큰 동안 반복''
'''do''' j := j - 1 '''while''' A[j] > pivot
''// 인덱스 교차 시 반환''
'''if''' i >= j '''then''' '''return''' j
''// 왼쪽, 오른쪽 인덱스 요소 교환''
'''swap''' A[i] '''with''' A[j]
```
전체 배열은 `quicksort(A, 0, length(A) - 1)`로 정렬된다.
호어 방식은 평균적으로 로무토 분할 방식보다 3배 적은 교환을 수행하여 더 효율적이며, 모든 값이 같을 때도 균형 분할을 생성한다.[9]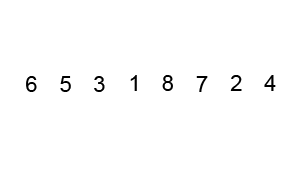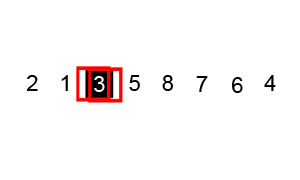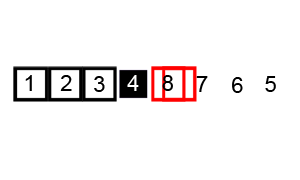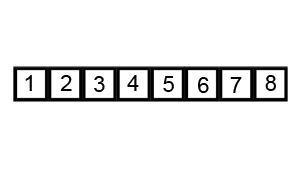
i, j) 위치, 검은색 윤곽선은 정렬된 요소, 채워진 검은색 사각형은 비교 대상 값(피벗).
3. 2. 피벗 선택
퀵 정렬의 성능은 피벗(pivot)을 어떻게 선택하느냐에 따라 크게 달라진다. 최악의 경우는 피벗이 항상 가장 작거나 큰 값으로 선택되는 경우이다. 예를 들어 이미 정렬된 배열에서 첫 번째나 마지막 요소를 피벗으로 선택하면 이러한 경우가 발생한다.[14]
피벗 선택을 개선하는 방법은 다음과 같다:
피벗을 선택할 때 정수 오버플로에도 주의해야 한다. 하위 배열의 경계 인덱스가 매우 크면, 중간 인덱스를 계산할 때 `(lo + hi) / 2`와 같은 표현식은 오버플로를 일으켜 잘못된 피벗 인덱스를 반환할 수 있다. 이를 방지하기 위해 `lo + (hi - lo) / 2`와 같이 더 복잡한 계산식을 사용해야 한다.
3. 3. 최적화 기법
퀵 정렬의 최적화 기법은 다음과 같다.4. 복잡도
:
퀵 정렬은 일반적으로 평균 의 시간 복잡도와 에서 사이의 공간 복잡도를 가진다. 자세한 내용은 시간 복잡도 및 공간 복잡도 하위 섹션을 참조하면 된다.
4. 1. 시간 복잡도
퀵 정렬의 시간 복잡도는 분할의 효율성에 크게 좌우되며, 최적, 평균, 최악의 경우로 나누어 분석할 수 있다.
최적의 경우 (Best Case):
평균적인 경우 (Average Case):
최악의 경우 (Worst Case):
최악의 경우 회피:최악의 경우를 방지하기 위해 다음과 같은 피벗 선택 전략을 사용할 수 있다.
추가적인 개선:
4. 2. 공간 복잡도
퀵 정렬이 사용하는 공간은 사용된 버전에 따라 달라진다.
제자리 정렬 방식의 퀵 정렬은 다음과 같은 전략을 사용하여 신중하게 구현했을 때 최악의 경우에도 공간 복잡도가 이다.
제자리, 불안정 분할을 사용하는 퀵 정렬은 재귀 호출을 하기 전에 상수 추가 공간만 사용한다. 퀵 정렬은 각 중첩 재귀 호출에 대한 상수 양의 정보를 저장해야 한다. 최상의 경우에는 최대 번의 중첩 재귀 호출을 수행하므로 공간을 사용한다. 그러나 재귀 호출을 제한하는 세지윅의 트릭이 없으면 최악의 경우 퀵 정렬은 번의 중첩 재귀 호출을 수행하고 의 보조 공간이 필요할 수 있다.
비트 복잡성 관점에서 보면, ''lo'' 및 ''hi''와 같은 변수는 상수 공간을 사용하지 않는다. 개의 항목 목록을 인덱싱하는 데 비트가 소요된다. 각 스택 프레임에 이러한 변수가 있기 때문에, 세지윅의 트릭을 사용하는 퀵 정렬은 비트의 공간이 필요하다. 이 공간 요구 사항은 그다지 심각하지 않지만, 목록에 고유한 요소가 포함된 경우 최소 비트의 공간이 필요하다.
또 다른 덜 일반적인, 제자리가 아닌 퀵 정렬 버전은 작업 저장소에 공간을 사용하며 안정 정렬을 구현할 수 있다. 작업 저장소를 사용하면 입력 배열을 안정적인 방식으로 쉽게 분할한 다음, 후속 재귀 호출을 위해 입력 배열에 다시 복사할 수 있다. 세지윅의 최적화는 여전히 적절하다.
5. 변형
퀵 정렬은 분할 정복 방식을 사용하여 태스크 병렬 처리(task parallelism)를 통해 쉽게 병렬화할 수 있다. 크기가 n인 배열을 이상적인 피벗으로 분할한다고 가정하면, 병렬 퀵 정렬은 O(n log n) 작업으로 O(log2 n) 시간에 O(n)의 추가 공간을 사용하여 정렬할 수 있다.[20][21] 그러나 퀵 정렬은 병합 정렬과 같은 다른 정렬 알고리즘에 비해 병렬화가 복잡하다는 단점이 있다.[22]
단일 피벗 대신 s-1개의 피벗을 사용하여 입력을 s개의 하위 배열로 분할하는 멀티 피벗 퀵 정렬(multiquicksort)이 있다.[30] 1999년에 프로세서 캐시를 효율적으로 사용하도록 조정된 멀티 피벗 퀵 정렬은 명령어 수가 약 20% 증가했지만 시뮬레이션 결과 매우 큰 입력에서 더 효율적인 것으로 나타났다. 2009년에는 Yaroslavskiy가 개발한 2중 피벗 퀵 정렬 버전[31]이 Java 7에서 기본형 배열을 정렬하는 표준 알고리즘으로 구현되었다.[32][33] 이 알고리즘의 성능 이점은 대부분 캐시 성능과 관련이 있으며,[34] 실험 결과에 따르면 3-피벗 변형이 최신 기계에서 더 나은 성능을 보일 수 있다.[35][36]
디스크 파일 정렬을 위한 외부 퀵 정렬도 가능하다. 이 방법은 외부 병합 정렬보다 느리지만 추가 디스크 공간이 필요하지 않다. 4개의 버퍼(입력 2개, 출력 2개)를 사용하며, 파일의 양쪽 끝에서 데이터를 읽고 쓴다. 평균적으로 파일에 대한 통과 횟수는 약 이지만, 최악의 경우 N 통과이다.[37]
기수 정렬과 퀵 정렬을 결합한 다중 키 퀵 정렬은 배열에서 요소를 선택하고 문자열의 첫 번째 문자를 기준으로 나머지 요소를 세 개의 집합으로 분할한다. "작은" 및 "큰" 분할은 같은 문자를 기준으로, "같은" 분할은 다음 문자를 기준으로 재귀적으로 정렬한다. W 비트 길이의 바이트 또는 단어를 사용할 때 최상의 경우는 O(KN)이고 최악의 경우는 O(2KN) 또는 최소 O(N2)이다.[38]
비교 기반 정렬 알고리즘에서 비교 횟수를 최소화하려면 각 비교에서 얻는 정보의 양을 최대화해야 한다. 이는 잦은 분기 예측 오류를 유발할 수 있다.[39] BlockQuicksort[40]는 퀵 정렬 계산을 재배열하여 예측 불가능한 분기를 데이터 종속성으로 변환한다. 입력은 데이터 캐시에 맞는 크기의 블록으로 나뉘고, 교환할 요소의 위치는 두 개의 배열에 저장된다. 두 번째 패스에서 요소가 교환되며, 두 루프 모두 종료 테스트라는 하나의 조건부 분기만 가진다.[41]
퀵 정렬에는 입력의 k번째로 작은 요소 또는 가장 큰 요소를 분리하는 여러 변형이 존재한다. 퀵 정렬은 피벗 선택, 배열 분할, 재귀를 통해 정렬을 수행한다. 배열 분할 방법에는 다양한 변형이 있으며(예: Dual-pivot Quicksort[31]), 분할 후 요소 수가 일정 임계값 미만이면 삽입 정렬과 같은 다른 정렬로 전환하는 기법도 있다.
6. 다른 알고리즘과의 관계
퀵 정렬은 이진 트리 정렬의 공간 최적화 버전으로 볼 수 있다. 이진 트리 정렬이 명시적인 트리에 항목을 순차적으로 삽입하는 대신, 퀵 정렬은 재귀 호출을 통해 암시적인 트리에 항목을 동시에 구성한다. 두 알고리즘은 동일한 비교를 수행하지만 순서가 다르다.
퀵 정렬의 가장 직접적인 경쟁자는 힙 정렬이다. 힙 정렬은 단순하고 최악의 경우에도 $O(n \log n)$ 실행 시간을 보장한다는 장점이 있지만, 일반적으로 참조 지역성이 좋지 않아 제자리 퀵 정렬보다 평균 실행 시간이 느리다고 알려져 있다.[27] 그러나 이 결과에 대해서는 반대되는 주장도 존재한다.[28][29] 퀵 정렬은 잘못된 피벗을 선택하면 성능이 $O(n^2)$로 저하될 수 있다는 단점이 있는데, 인트로 정렬은 이러한 경우에 힙 정렬로 전환하여 이 문제를 해결한다.
퀵 정렬은 병합 정렬과도 경쟁한다. 병합 정렬은 안정 정렬이며 최악의 경우에도 $O(n \log n)$ 성능을 보장한다. 그러나 병합 정렬은 제자리 정렬이 아니기 때문에 배열에서 작동할 때 $O(n)$의 보조 공간이 필요하다. 반면, 퀵 정렬은 제자리 분할 및 꼬리 재귀를 사용하면 $O(\log n)$의 추가 공간만 필요하다. 병합 정렬은 연결 리스트 정렬에 매우 효율적이며, 퀵 정렬은 연결 리스트에서는 피벗 선택 문제로 인해 성능이 저하될 수 있다.
선택 알고리즘은 숫자 목록에서 $k$번째로 작은 숫자를 찾는 문제이다. 퀵 정렬과 유사한 방식으로 작동하는 퀵셀렉트 알고리즘은 평균 $O(n)$ 시간에 이 문제를 해결할 수 있다. 퀵셀렉트의 변형인 중앙값의 중앙값 알고리즘은 피벗을 더 신중하게 선택하여 최악의 경우에도 $O(n)$ 시간을 보장한다. 이 피벗 선택 전략을 퀵 정렬에 적용하여 $O(n \log n)$ 시간을 갖는 변형을 만들 수 있지만, 피벗 선택 오버헤드가 커서 실제로 사용되지는 않는다.
7. 구현 예제
C, C++, C#, Java, Python 등 다양한 프로그래밍 언어로 퀵 정렬을 구현할 수 있다.
- C
```c
/**
- 값을 교환합니다.
- @param x - 교환할 데이터의 포인터
- @param y - 교환할 데이터의 포인터
- @param sz - 데이터 크기
- /
void
swap(
void* x,
void* y,
size_t sz
) {
char* a = x;
char* b = y;
while (sz > 0) {
char t = *a;
- a++ = *b;
- b++ = t;
sz--;
}
}
/** 분할 함수
- 배열을 피벗을 기준으로 분할하고 분할 위치를 반환합니다.
- @param a - 분할할 배열
- @param cmp - 비교 함수에 대한 포인터
- @param sz - 데이터 크기
- @param n - 요소 수
- @returns 분할 위치를 나타내는 포인터
- /
void*
partition(
void* a,
int (*cmp)(void const*, void const*),
size_t sz,
size_t n
) {
// void* 에 대해 직접 포인터 연산을 할 수 없으므로 미리 char* 로 변환합니다.
char* const base = a;
if (n <= 1) return base + sz;
char* lo = base;
char* hi = &base[sz * (n - 1)];
char* m = lo + sz * ((hi - lo) / sz / 2);
// m 이 median-of-3 을 가리키도록 정렬
if (cmp(lo, m) > 0) {
swap(lo, m, sz);
}
if (cmp(m, hi) > 0) {
swap(m, hi, sz);
if (cmp(lo, m) > 0) {
swap(lo, m, sz);
}
}
while (1) {
while (cmp(lo, m) < 0) lo += sz; // 피벗 이상의 요소를 아래에서 찾습니다.
while (cmp(m, hi) < 0) hi -= sz; // 피벗 이하의 요소를 위에서 찾습니다.
if (lo >= hi) return hi + sz;
swap(lo, hi, sz);
// 피벗이 스왑된 경우, 스왑 대상을 가리키도록 m 을 업데이트합니다.
if (lo == m) {
m = hi;
} else if (hi == m) {
m = lo;
}
lo += sz;
hi -= sz;
}
}
/** 퀵 정렬
- @param a - 정렬할 배열
- @param cmp - 비교 함수에 대한 포인터
- @param sz - 데이터 크기
- @param n - 요소 수
- /
void
quicksort(
void* a,
int (*cmp)(void const*, void const*),
size_t sz,
size_t n
) {
if (n <= 1) return;
char* p = partition(a, cmp, sz, n);
char* const base = a;
size_t n_lo = (p - base) / sz;
size_t n_hi = (&base[sz * n] - p) / sz;
quicksort(a, cmp, sz, n_lo); // 왼쪽을 정렬합니다.
quicksort(p, cmp, sz, n_hi); // 오른쪽을 정렬합니다.
}
```
`cmp(x, y)`는 `x < y`인 경우 음수, `x = y`인 경우 0, `x > y`인 경우 양의 정수를 반환하는 함수이다.
- C++
```cpp
void quickSort(int arr[], int left, int right) {
int i = left, j = right;
int pivot = arr[(left + right) / 2];
int temp;
while (i <= j)
{
while (arr[i] < pivot) i++; // arr[i] ≥ pivot 일 때까지, left에서 오른쪽 방향으로 탐색
while (arr[j] > pivot) j--; // arr[j] ≤ pivot 일 때까지, right에서 왼쪽 방향으로 탐색
if (i <= j) // 큰 값이 작은 값보다 왼쪽에 있으면
{
// SWAP(arr[i], arr[j])
temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
i++;
j--;
}
}
/* 재귀(recursion) */
if (left < j) quickSort(arr, left, j);
if (i < right) quickSort(arr, i, right);
}
```
```pascal
function partition(arr, left, right, pivot_index)
pivot_value := arr[pivot_index]
swap(arr[pivot_index], arr[right]) // 피벗을 끝으로 옮겨 놓는다.
stored_index := left
for i in range (left,right) // left에서부터 (right-1)까지
if arr[i] ≤ pivot_value then
swap(arr[stored_index], arr[i])
stored_index := stored_index + 1
swap(arr[right], arr[stored_index]) // 피벗을 두 리스트 사이에 위치시킨다.
return stored_index
```
내부 분할 알고리즘은 주어진 배열에서 `pivot_index`에 위치한 값보다 작은 값들을 리스트의 앞쪽에, 큰 값들을 리스트의 맨 뒤에 배치하여 `left`와 `right` 위치 사이의 원소들을 두 개로 분할한다. 분할된 두 리스트 사이에 피벗을 위치시키면 피벗의 위치가 정해진다. 피벗 값은 임시로 리스트의 맨 뒤에 저장해놓기 때문에 중간에 피벗의 위치가 바뀌지 않는다.
```pascal
function quicksort(a, left, right)
if right > left then
select a pivot value for a[pivot_index]
pivot_NewIndex := partition(a, left, right, pivot_index)
quicksort(a, left, pivot_NewIndex-1)
quicksort(a, pivot_NewIndex+1, right)
```
```vb
Private Function QR(a() As Long, left As Long, right As Long)
Dim pivot, left_hold, right_hold As Long
left_hold = left
right_hold = right
pivot = a(left)
Do While (left < right)
Do While ((a(right) >= pivot) And (left < right))
right = right - 1
Loop
If left <> right Then
a(left) = a(right)
End If
Do While ((a(left) <= pivot) And (left < right))
left = left + 1
Loop
If left <> right Then
a(right) = a(left)
right = right - 1
End If
Loop
a(left) = pivot
pivot = left
left = left_hold
right = right_hold
If left < pivot Then
Call QR(a(), left, pivot - 1)
End If
If right > pivot Then
Call QR(a(), pivot + 1, right)
End If
End Function
Private Function QS(a() As Long, count As Long)
Call QR(a(), 0, count - 1)
End Function
```
- F#
```f#
let rec quicksort = function
| [] -> []
| pivot::rest ->
let left, right = rest |> List.partition (fun i -> i < pivot)
quicksort left @ [pivot] @ quicksort right
// Test
printfn "%A" (quicksort [3;5;2;1;4;])
```
```haskell
quicksort [] = []
quicksort (p:tl) = quicksort [ x | x <- tl, x <= p ] ++ [p] ++ quicksort [ x | x <- tl, x > p ]
```
OCaml과 비교를 쉽게 하기 위한 버전은 아래와 같다.
```haskell
quicksort [] = []
quicksort (pivot:rest) =
let left = [x| x <- rest, x <= pivot]
right = [x| x <- rest, x > pivot]
in quicksort left ++ [pivot] ++ quicksort right
```
- Python
```python
from typing import Any
from collections.abc import MutableSequence, Callable
def median3(x, y, z):
return max(min(x, y), min(max(x, y), z))
def partition(seq: MutableSequence[Any], keyFn: Callable
pivot = median3(keyFn(seq[first]), keyFn(seq[first + (last - first) // 2]), keyFn(seq[last]))
while True:
while keyFn(seq[first]) < pivot:
first += 1
while pivot < keyFn(seq[last]):
last -= 1
if first >= last:
return last + 1
seq[first], seq[last] = seq[last], seq[first]
first += 1
last -= 1
def quicksort(seq: MutableSequence[Any], keyFn: Callable
def quicksortImpl(seq: MutableSequence, keyFn: Callable
while first < last:
p = partition(seq, keyFn, first, last)
if (p - first) < (last - p):
quicksortImpl(seq, keyFn, first, p - 1)
first = p
else:
quicksortImpl(seq, keyFn, p, last)
last = p - 1
quicksortImpl(seq, keyFn, 0, len(seq) - 1)
```
```python
def quicksort(x):
if len(x) <= 1:
return x
pivot = x[len(x) // 2]
less = []
more = []
equal = []
for a in x:
if a < pivot:
less.append(a)
elif a > pivot:
more.append(a)
else:
equal.append(a)
return quicksort(less) + equal + quicksort(more)
```
```python
def partition(arr, start, end):
pivot = arr[start]
left = start + 1
right = end
done = False
while not done:
while left <= right and arr[left] <= pivot:
left += 1
while left <= right and pivot <= arr[right]:
right -= 1
if right < left:
done = True
else:
arr[left], arr[right] = arr[right], arr[left]
arr[start], arr[right] = arr[right], arr[start]
return right
def quick_sort(arr, start, end):
if start < end:
pivot = partition(arr, start, end)
quick_sort(arr, start, pivot - 1)
quick_sort(arr, pivot + 1, end)
return arr
```
- 스칼라
```scala
def quickSort(arr:Array[Int]):Array[Int] = {
if (arr.length <= 1) return arr
val pivot = arr(arr.length / 2)
var left, right, equal = Array[Int]()
for (a <- arr) {
if (a < pivot) left = left :+ a
else if (a > pivot) right = right :+ a
else equal = equal :+ a
}
quickSort(left) ++ equal ++ quickSort(right)
}
```
```javascript
/**
- 퀵 정렬
- 시간 복잡도: 최악 - O(n2), 최선 - O(nlogn), 평균 - O(nlogn)
- 공간 복잡도: O(1)
- @param {Array} arr
- @param {int} left
- @param {int} right
- @code
var arr = [ 4, 5, 1, 2, 11, 8, 3, 1, 2, 5 ];
quicksort(arr, 0, arr.length-1);
- /
var quicksort = function(arr, left, right) {
if (left < right) {
//기준점을 찾고 기준점을 중심으로 더 작은수, 더 큰수 분류
var i = position(arr, left, right);
//기준점 기준 좌측 정렬
quicksort(arr, left, i - 1);
//기준점 기준 우측 정렬
quicksort(arr, i + 1, right);
}
return arr;
};
var position = function(arr, left, right) {
var i = left;
var j = right;
var pivot = arr[left];
//제자리 더 큰수/더 작은 수 좌우 배치.
while (i < j) {
while (arr[j] > pivot) j--;
while (i < j && arr[i] <= pivot) i++;
tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
arr[left] = arr[j];
arr[j] = pivot;
return j;
}
```
- Scheme
```scheme
(require-extension srfi-1) ; SRFI 1 호출 방법은 구현에 따라 다름 (경우에 따라 기본값). 이는 Chicken Scheme의 예시입니다.
(define (qsort f ls)
(if (null? ls)
'()
(let ((x (car ls)) (xs (cdr ls)))
(let ((before
(qsort f (filter (lambda (y) ; filter는 SRFI 1의 절차
;; compose는 Chicken, Gauche, Guile, Racket 등에 있는 "합성 함수를 만드는" 절차입니다.
;; 자세한 내용은 Paul Graham의 On Lisp를 참조하십시오.
;; https://www.asahi-net.or.jp/~kc7k-nd/onlispjhtml/returningFunctions.html
((compose not f) x y)) xs)))
(after
(qsort f (filter (lambda (y) ; filter는 SRFI 1의 절차
(f x y)) xs))))
(append before (cons x after))))))
참조
[1]
웹사이트
Sir Antony Hoare
http://www.computerh[...]
Computer History Museum
2015-04-22
[2]
간행물
Algorithm 64: Quicksort
[3]
서적
The Algorithm Design Manual
https://books.google[...]
Springer
[4]
서적
Algorithms, Abstraction and Implementation
[5]
간행물
Interview: An interview with C.A.R. Hoare
[6]
웹사이트
My Quickshort interview with Sir Tony Hoare, the inventor of Quicksort
http://anothercasual[...]
Marcelo M De Barros
2015-03-15
[7]
간행물
Algorithms 402: Increasing the Efficiency of Quicksort
1970-11-01
[8]
서적
Beautiful Code: Leading Programmers Explain How They Think
O'Reilly Media
[9]
웹사이트
Quicksort Partitioning: Hoare vs. Lomuto
https://cs.stackexch[...]
2015-08-03
[10]
간행물
A killer adversary for quicksort
https://www.cs.dartm[...]
1999-04-10
[11]
학위논문
Java 7's Dual Pivot Quicksort
https://kluedo.ub.un[...]
Technische Universität Kaiserslautern
2012
[12]
서적
Introduction to Algorithms
[13]
간행물
Quicksort
1962-01-01
[14]
서적
Proceedings of the 2014 ACM SIGMOD International Conference on Management of Data
ACM
2014-06-18
[15]
간행물
Engineering a sort function
http://citeseer.ist.[...]
[16]
문서
qsort.c in GNU libc
https://www.cs.colum[...]
[17]
웹사이트
http://www.ugrad.cs.[...]
[18]
서적
Programming Pearls
Addison-Wesley Professional
[19]
간행물
The Influence of Caches on the Performance of Sorting
[20]
웹사이트
Quicksort and Sorting Lower Bounds
https://www.cs.cmu.e[...]
[21]
간행물
Quicksort Partition via Prefix Scan
http://www.drdobbs.c[...]
[22]
서적
Algorithms sequential & parallel: a unified approach
https://books.google[...]
Prentice Hall
[23]
학술대회
Parallelized Quicksort and Radixsort with Optimal Speedup
[24]
문서
[25]
서적
Algorithms in C: Fundamentals, Data Structures, Sorting, Searching, Parts 1–4
https://books.google[...]
Pearson Education
1998-09-01
[26]
간행물
Implementing Quicksort programs
[27]
학술대회
Worst-Case Efficient Sorting with QuickMergesort
2019-01-07
[28]
웹사이트
Sorting revisited
http://www.azillionm[...]
azillionmonkeys.com
[29]
웹사이트
Heapsort, Quicksort, and Entropy
http://www.inference[...]
2005-12
[30]
학술대회
Average case analysis of Java 7's dual pivot quicksort
[31]
웹사이트
Dual-Pivot Quicksort
http://iaroslavski.n[...]
2009
[32]
서적
Engineering Java 7's Dual Pivot Quicksort Using MaLiJAn
Society for Industrial and Applied Mathematics
2013-01-07
[33]
웹사이트
Arrays
http://docs.oracle.c[...]
Oracle
2014-09-04
[34]
학술논문
Why Is Dual-Pivot Quicksort Fast?
2015-11-03
[35]
학술대회
Multi-Pivot Quicksort: Theory and Experiments
[36]
학회
Multi-Pivot Quicksort: Theory and Experiments
https://lusy.fri.uni[...]
2014-02-07
[37]
논문
An efficient external sorting with minimal space requirement
1982
[38]
문서
Parallel Unification: Practical Complexity
http://david.wardpow[...]
Australasian Computer Architecture Workshop, Flinders University
1995-01
[39]
학회
How Branch Mispredictions Affect Quicksort
https://www.cs.auckl[...]
2006-09-11
[40]
간행물
BlockQuicksort: How Branch Mispredictions don't affect Quicksort
2016-04-22
[41]
웹사이트
Changing std::sort at Google's Scale and Beyond
https://danlark.org/[...]
2022-04-20
[42]
학회
"The average case analysis of Partition sorts"
http://www.cs.nyu.ed[...]
Springer Verlag
2004-09-14
[43]
문서
「先頭未満/以上」で分割してしまった場合、無限再帰による[[スタックオーバーフロー]]も起こりうる
[44]
웹사이트
Cによる実装例
https://programming-[...]
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com
